4 Verteilungen
Im letzten Kapitel sind wir darauf eingegangen, dass man Zufallsexperimente mit einer Zufallsvariable und dessen Verteilung zusammenfassen kann. Natürlich eignet sich nicht jede Verteilung, um jedes Zufallsexperiment zu beschreiben. In Beispiel 3.2 wäre es zum Beispiel wenig situationsbezogen gewesen, die Augenzahl eines klassischen Würfel über eine Zufallsvariable
Dementsprechend müssen wir darauf achten, dass der kleinste Wertebereich
Nach dieser Bezeichnung ist die Zufallsvariable
Innerhalb der Klassen der diskreten Zufallsvariablen gibt es allerdings noch eine Vielzahl an weiteren Verteilungen, die unterschiedlich Wahrscheinlichkeiten zulassen. In diesem Kapitel werden wir einige davon kennenlernen. Außerdem werden wir auch die Klasse der absolutstetigen Zufallsvariablen erkunden. Diese führen uns in den Bereich eines überabzählbaren Wertebereichs
4.1 Diskrete Zufallsvariablen
Um die unterschiedlichen diskreten Verteilungen kennenzulernen, führen wir den Begriff der Zähldichte ein. Da die Zähldichte auf sehr simple Weise mit der Verteilungsfunktion
Definition 4.1 (Zähldichte) Es sei
Beispiel 4.1 (Diskrete Gleichverteilung) Die Zähldichte der diskreten Gleichverteilung auf einer Menge $C = { x_1, , x_N }$ ist gegeben als
Beispiel 4.2 (Geometrische Verteilung) Die geometrischen Verteilung besitzt die Zähldichte
Nehmen wir an, dass ein Paar versucht, ein Mädchen zu bekommen. Außerdem ist es für dieses Paar scheinbar logistisch2 möglich so lange Kinder zu kriegen, bis es ein Mädchen bekommt. Wir interessieren uns nun für die Fragestellung, wie wahrscheinlich es ist, dass das Paar genau 3 Jungs bekommt, bevor das erste Mädchen geboren wurde und modellieren dies mit einer geometrischen Verteilung.
Es sei also
Beispiel 4.3 (Binomialverteilung) Die Binomialverteilung besitzt die Zähldichte
Betrachten wir wieder das Paar aus Beispiel 4.2 und nehmen an, dass das Paar unabhängig vom Geschlecht nun 4 Kinder bekommen hat. Nun wollen wir untersuchen, wie wahrscheinlich es ist, dass das Paar mindestens 2 Mädchen bekommen hat. Dazu definieren wir
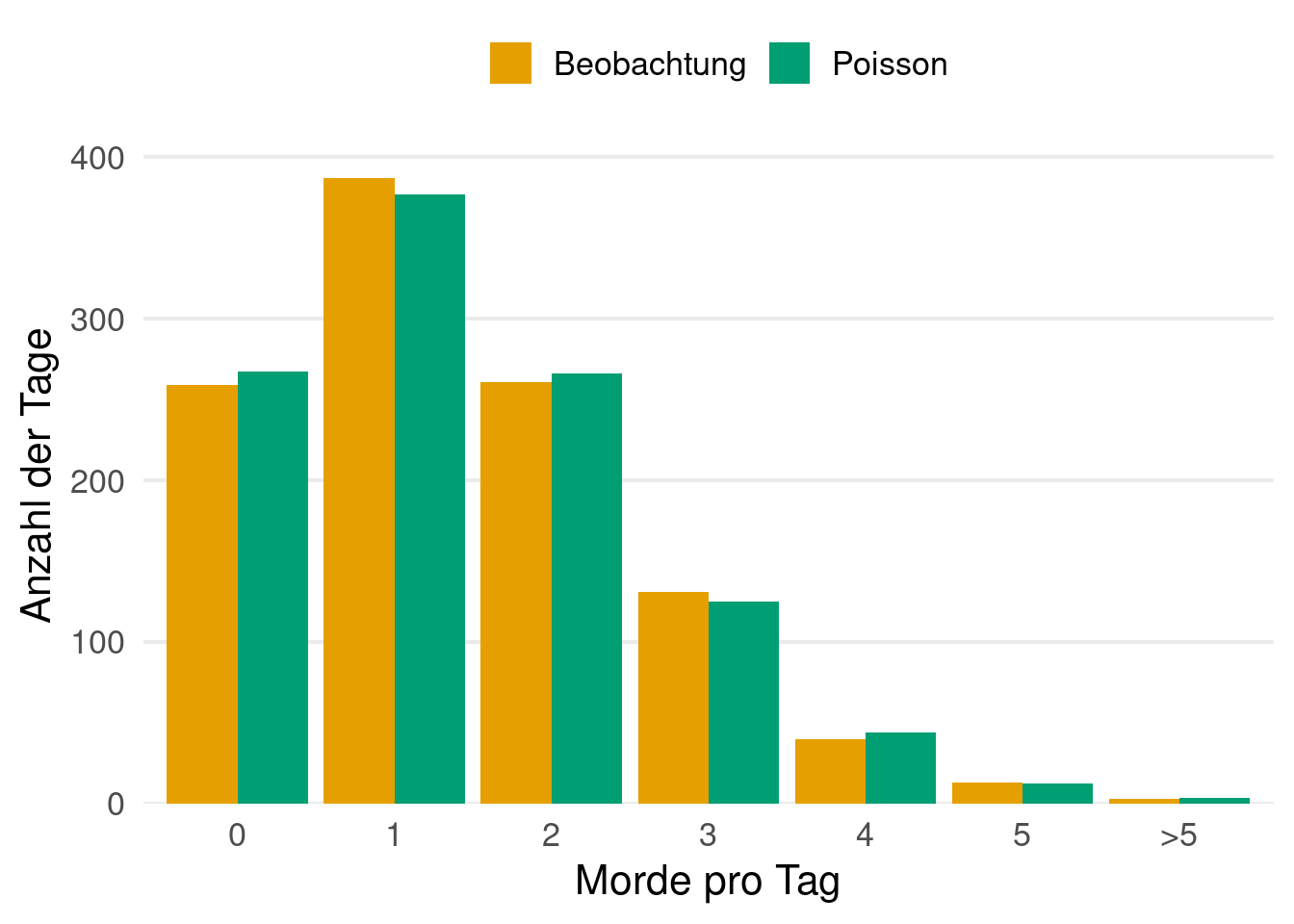
Beispiel 4.4 (Poisson Verteilung) Die Poissonverteilung besitzt die Zähldichte
Insgesamt gab es 1.545 Vorfälle über einen Zeitraum von 1.095 Tagen. Dies führt zu einer durchschnittlichen Rate von
Bemerkung 4.1
All diese Zähldichten haben zwei Dinge gemeinsam:
Die Summe über alle
Nach dem Poissonschen Approximationssatz bzw. dem Gesetz der seltenen Ereignisse lässt sich die Binomialverteilung für große
4.2 Absolutstetige Zufallsvariablen
Die bisherige Klasse von Verteilungen ist leider keine adäquate Wahl für viele Anwendungsfälle. Wollen wir beispielsweise die (zufällige) Ankunftszeit eines Freundes an einem vereinbarten Treffpunkt beschreiben, so stellen wir fest, dass es überabzählbar viele mögliche Ankunftszeiten gibt (sofern wir Zeit als ein Kontinuum auffassen).
Somit brauchen wir eine Zufallsvariable
Deswegen müssen wir uns mit einer Hilfsfunktion begnügen, die ein Analogon zur Zähldichte
Definition 4.2 (Absolutstetigkeit, Dichte) Die Verteilung einer Zufallsvariable
Genau wie es im diskreten Fall mit der Zähldichte funktioniert hat, können wir im absolutstetigen Fall eine Verteilung eindeutig über die Dichtefunktion charakterisieren. Zudem können wir beliebige Wahrscheinlichkeiten mittels
Bemerkung 4.2
Absolutstetige Zufallsvariablen sind nicht die einzigen Zufallsvariablen mit überabzählbarem Wertebereich
Analog zur Bemerkung 4.1 muss die Zähldichte die folgenden Eigenschaften erfüllen:
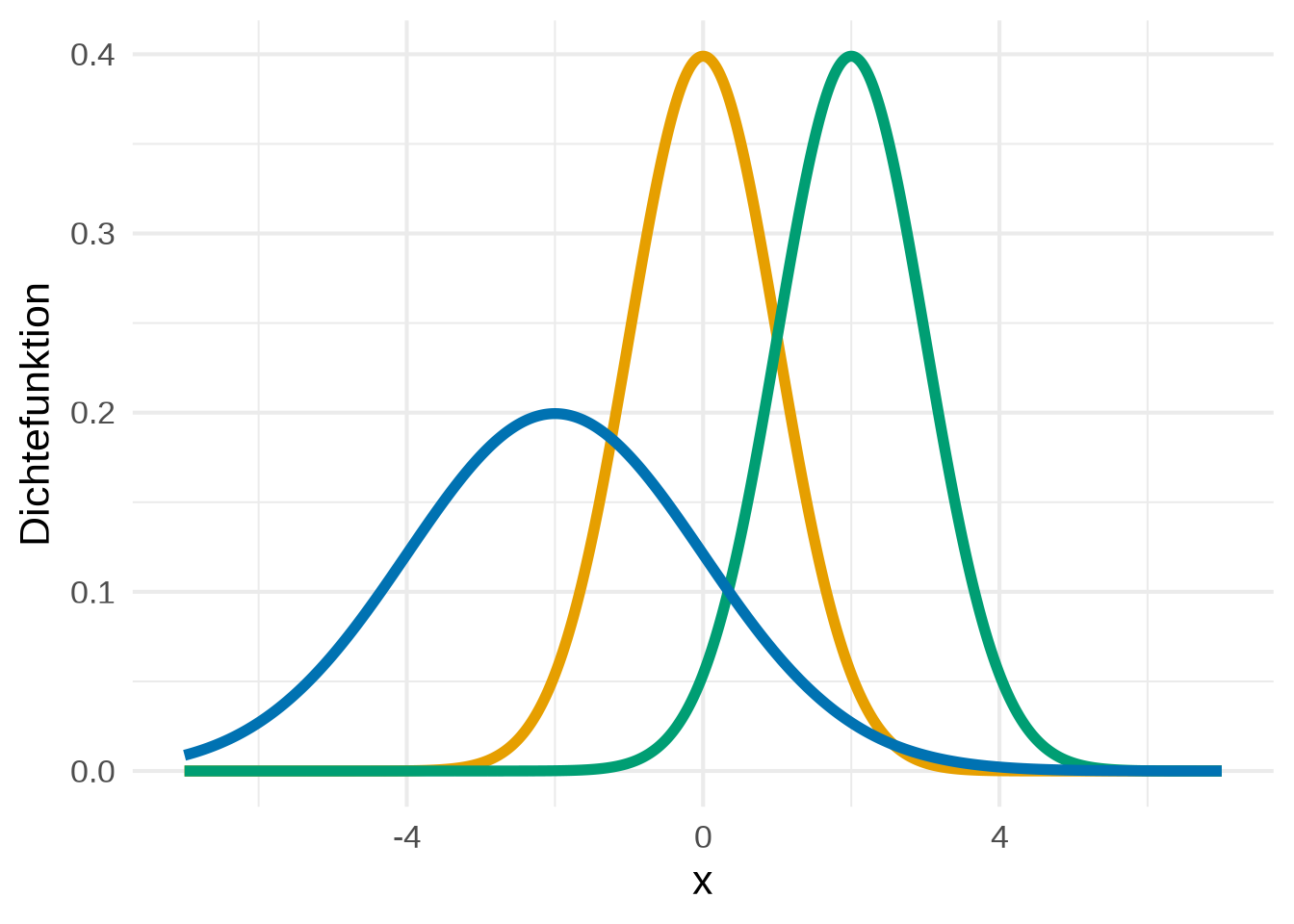
Beispiel 4.5 (Normalverteilung) Die Normalverteilung zählt zu den wichtigsten Verteilungen in der Stochastik. Ihre Dichte ist gegeben durch
Betrachtet man die Dichten der Normalverteilung in Abbildung 4.2, so lässt sich erkennen, dass ein Großteil der Fläche zwischen Funktion und
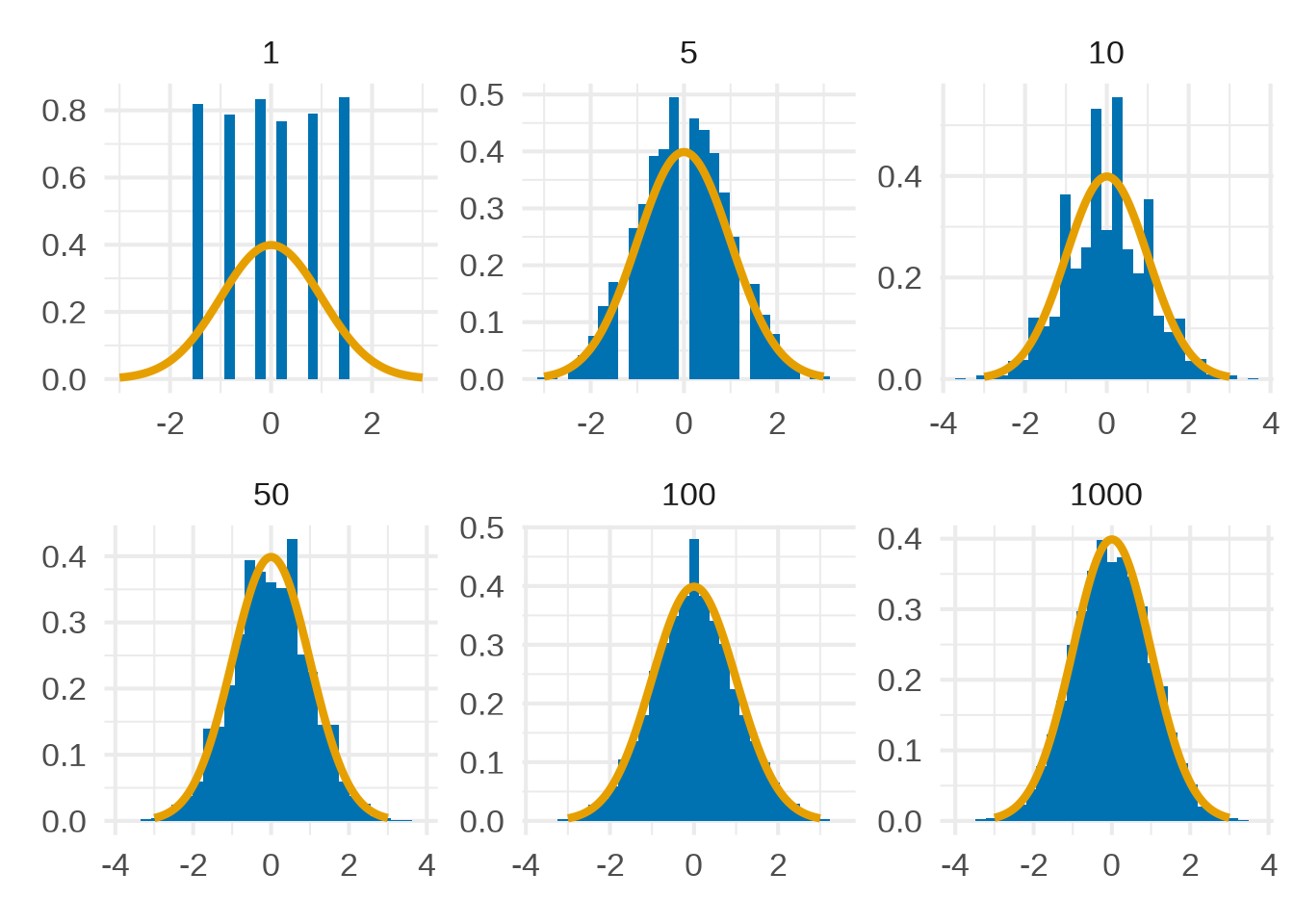
Ein weiterer Grund für die Wichtigkeit der Normalverteilung ist der zentrale Grenzwertsatz (ZGWS), den ich hier nur anschneiden möchte. Wir werden in einem späteren Kapitel ausführlicher über den ZGWS reden. Grob formuliert besagt der Satz, dass ich unter sehr milden Bedingungen eine Summe von Zufallsvariablen
Die Folge
Nehmen wir nun an, dass wir einen Würfel
Beispiel 4.6 (Exponentialverteilung) Eine weitere wichtige absolutstetige Verteilung ist die Exponentialverteilung mit Dichtefunktion
Streng genommen ist die Verteilung der jeweiligen Zufallsvariable diskret. Jedoch werden die Zufallsvariablen häufig auch so genannt.↩︎
Anlässlich der Anmerkung meiner Freundin sei an dieser Stelle erwähnt, dass mir bewusst ist, dass zum Kinderkriegen mehr als nur “logistische’’ Überlegungen dazugehören. Das ist hier natürlich alles nur grob vereinfacht dargestellt.↩︎
Für mich persönlich ist hier verblüffend, wie gut man Beobachtungen durch geeignete mathematische Modelle beschreiben kann. An sich ist es allerdings auch gut, dass die Poissonverteilung so gut passt, da dies als Indiz dafür dienen kann, dass die Mordrate halbwegs konstant ist und kein Serienmörder o.ä. unterwegs ist.↩︎
Außerdem hätte die Verteilungsfunktion solch einer Zufallsvariable überabzählbar viele Sprungstellen. Dies ist aber unmöglich, da eine monotone Funktion höchstens abzählbar viele Sprungstellen haben kann. Danke an Marco Oesting für diesen Hinweis zur technischen Untermalung der obigen Begründung.↩︎