8 Konvergenz von Zufallsvariablen

Aus den Analysisgrundvorlesungen kennt man üblicherweise das Konzept der punktweisen Konvergenz von Funktionsfolgen $(f_n)_{n \in \mathbb{N}}$, wobei $f_n: D \rightarrow \mathbb{R}$ für alle $n \in \mathbb{N}$ eine reellwertige Funktion ist. Und wir schreiben $f_n \rightarrow f$ punktweise, falls für alle $x \in D$ gilt $\lim_{n \rightarrow \infty} f_n(x) = f(x)$.

Wie mittlerweile bekannt sein sollte, sind Zufallsvariablen auch nichts anderes als (messbare) Funktionen. Somit könnte man das Konzept genauso gut für Folgen $(X_n)_{n \in \mathbb{N}}$ von Zufallsvariablen $X_n: \Omega \rightarrow \mathbb{R}$ anwenden. Allerdings haben wir auch schon mehrfach festgestellt, dass uns die konkreten Stellen $\omega \in \Omega$ im Definitionsbereich von $X_n$ nur wenig interessieren. Wir haben auch festgestellt, dass $X_n(\omega)$ für konkrete $\omega$ sogar sehr wilde Dinge tun kann, solange die entsprechenden $\omega$ eine Nullmenge bilden, d.h. für die Vereinigung $A$ aller Stellen $\omega$ an denen $X$ komische Dinge tut, gilt $\mathbb{P}(A) = 0$ (siehe Annahme 3.1 und Beispiel 3.2). Dementsprechend ergibt es auch für Konvergenzbetrachtungen Sinn, diese Nullmengen zu ignorieren. Dies führ uns zur fast sicheren Konvergenz.

Definition 8.1 (Fast sichere Konvergenz) Es sei $(X_n)_{n \in \mathbb{N}}$ eine Folge von Zufallsvariablen $X_n$. Wir sagen $X_n$ konvergiert fast sicher gegen eine Zufallsvariable $X$, falls \[\begin{align} \label{eq: fs Konvergenz} \mathbb{P}\big(\lim\limits_{n \rightarrow \infty} X_n = X \big) = 1 \tag{1} \end{align}\] für $n \rightarrow \infty$. In diesem Fall schreiben wir $X_n \stackrel{\text{f.s.}}{\longrightarrow} X$.

Auf den ersten Blick mag Gleichung $\eqref{eq: fs Konvergenz}$ etwas abstrakt wirken. Letztendlich komprimiert diese Gleichung lediglich die Beschreibung zu Beginn dieses Kapitels. Dennoch fällt es zunächst schwer, die Wahrscheinlichkeit in Gleichung $\eqref{eq: fs Konvergenz}$ zu berechnen, um die Definitionsvoraussetzung zu überprüfen. Glücklicherweise gibt es ein praktisches Theorem, das uns hilft, fast sichere Konvergenz auf andere Weise nachzuweisen.

Theorem 8.1 Es seien $X, X_1, \ldots$ beliebige Zufallsvariablen. Nun gilt $X_n \stackrel{\text{f.s.}}{\longrightarrow} X$ für $n \rightarrow \infty$, falls \[\begin{align} \label{eq: Bedingung fs Konvergenz} \sum_{n = 1}^{\infty} \mathbb{P}(\vert X_n - X \vert > \varepsilon) < \infty \tag{2} \end{align}\] für alle $\varepsilon > 0$.

Annahme 8.1

Damit die Bedingung $\eqref{eq: Bedingung fs Konvergenz}$ in Theorem 8.1 erfüllt sein kann, muss für alle $\varepsilon > 0$ gelten \[\begin{align} \label{eq: p Konvergenz} \mathbb{P}(\vert X_n - X \vert > \varepsilon) \rightarrow 0 \tag{3} \end{align}\] für $n \rightarrow \infty$. Dies bedeutet, dass die Wahrscheinlichkeit, dass $X_n$ und $X$ sich beliebig wenig unterscheiden, gegen Null geht.
Falls die Bedingung $\eqref{eq: p Konvergenz}$ erfüllt ist, spricht man auch davon, dass $X_n$ in Wahrscheinlichkeit gegen $X$ konvergiert. Wir stellen also fest, dass wegen Bedingung $\eqref{eq: Bedingung fs Konvergenz}$ gilt: Hinreichend schnelle Konvergenz in Wahrscheinlichkeit impliziert fast sichere Konvergenz (hinreichend schnell ist hierbei so zu verstehen, dass die Summe $\eqref{eq: Bedingung fs Konvergenz}$ endlich ist).

Beispiel 8.1 Es sei $X_n \sim$ U$(0, n^{-1})$ für alle $n \in \mathbb{N}$. Wir stellen fest, dass $X_1 \sim U(0, 1)$, $X_2 \sim U(0, 0{.}5)$, usw. Dementsprechend ist $X_n$ mit steigendem $n$ auf einem immer kleiner werdenden Intervall gleichverteilt. Da $n^{-1} \rightarrow 0$ für $n \rightarrow \infty$, lässt sich intuitiv überlegen, dass $X_n$ gegen die (langweilige konstante) Zufallsvariable $0$ konvergiert.

Nach Annahme 8.1 könnte diese Konvergenz im Sinne der Konvergenz in Wahrscheinlichkeit verlaufen und wenn dies hinreichend schnell passiert, dann können wir sogar fast sichere Konvergenz über Theorem 8.1 folgern. Rechnen wir also zunächst Bedingung $\eqref{eq: p Konvergenz}$ nach. Dazu sei $\varepsilon > 0$ und es gilt \[\begin{align*} \mathbb{P}(\vert X_n - 0 \vert > \varepsilon) = \mathbb{P}(X_n > \varepsilon) = \big(1 - n\varepsilon\big) \mathbb{1}\big\{ \varepsilon \in (0, n^{-1}) \big\} \rightarrow 0 \end{align*}\]
für $n \rightarrow \infty$. Also wissen wir, dass $X_n$ in Wahrscheinlichkeit gegen $0$ konvergiert. Außerdem ist wegen der Indikatorfunktion $\mathbb{1}\{\varepsilon \in (0, n^{-1})\}$ die Summe in Bedingung $\eqref{eq: Bedingung fs Konvergenz}$ als Summe von endlich vielen Termen auch endlich ist. Damit gilt $X_n \stackrel{\text{f.s.}}{\longrightarrow} 0$.

In Kapitel 6 haben wir den Erwartungswert $\mathbb{E}X$ einer Zufallsvariable $X$ kennengelernt und diesen als den Wert interpretiert, der “im Mittel’’ angenommen wird. Allerdings hat bereits Beispiel 6.1 gezeigt, dass diese Interpretation ein wenig hinkt. Schließlich haben wir dort festgestellt, dass wir für eine gewürfelten Zahl $X$ einen Erwartungswert von $\mathbb{E}X = 3{.}5$ erhalten. Allerdings ist es unmöglich eine $3{.}5$ zu würfeln (jedenfalls mit einem Standardwürfel).

Nachdem wir nun das Konzept von fast sicherer Konvergenz kennen, können wir unser Verständnis des Erwartungswertes aufpolieren.

Theorem 8.2 (Starkes Gesetz der großen Zahlen) Es seien $X_n$, $n \in \mathbb{N}$, unabhängige und identisch verteilte Zufallsvariablen. Dann existiert ein endlicher Erwartungswert $\mu = \mathbb{E}X_1 < \infty$ genau dann, wenn \[\begin{align} \frac{1}{n} \sum_{k = 1}^{n} X_k \stackrel{\text{f.s.}}{\longrightarrow} \mu \label{eq: SGGZ} \tag{4} \end{align}\] für $n \rightarrow \infty$.

Annahme 8.2

Somit kann man den Erwartungswert einer Zufallsvariable $X$ als arithmetisches Mittel von unendlich vielen, unabhängigen Kopien von $X$ betrachten.
Die Bezeichnung “starkes’’ Gesetz bezieht sich im Wesentlichen darauf, dass die Konvergenz $\eqref{eq: SGGZ}$ als fast sichere Konvergenz zu verstehen ist. Das schwache Gesetz der großen Zahlen versteht diese Konvergenz allerdings nur als Konvergenz in Wahrscheinlichkeit.

Beispiel 8.2 Mithilfe des SGGZ und der Überlegung $\mathbb{E}\mathbb{1}(A) = \mathbb{P}(A)$ für ein Ereignis $A \in \mathcal{F}$ erhält man leicht, dass für unabhängige Kopien $X_i$, $i \in \mathbb{N}$, der Zufallsvariable $X = \mathbb{1}(A)$ gilt \[\begin{align*} \frac{1}{n} \sum_{k = 1}^{n} X_k = \frac{\#\{ X_k = 1 \}}{n} \stackrel{\text{f.s.}}{\longrightarrow} \mathbb{P}(A), \end{align*}\] wobei $\#\{ X_k = 1 \}$ angibt, wie oft das Ereignis $A$ eingetreten ist. Somit gibt das starke Gesetz der großen Zahlen auch eine Begründung, warum man die relative Häufigkeit als Wahrscheinlichkeit interpretiert.

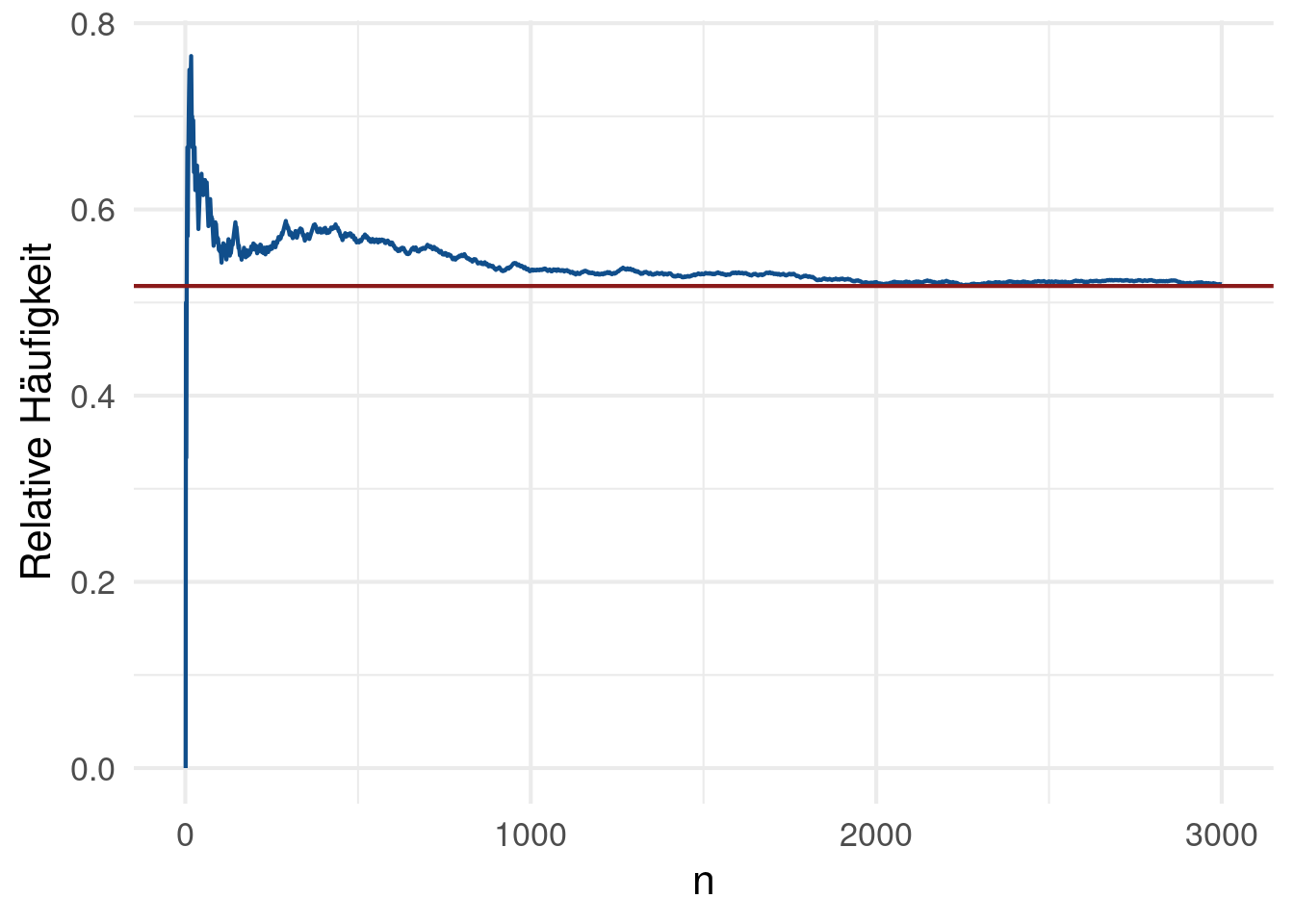
Konkreter können wir das folgende Würfelspiel betrachten. Ein Würfel wird maximal $4$ mal geworfen und wir gewinnen das Spiel, wenn wir eine $6$ würfeln. Wir definieren nun $X_k = \mathbb{1}\{ k\text{-tes Spiel gewonnen} \}$, $k = 1, \ldots, n$, wobei $n \in \mathbb{N}$. Somit gilt $X_k \sim$ Ber$(p)$ mit $p \approx 0{.}5177$ und wir nehmen an, dass die $X_k$ unabhängig voneinander sind. Nach dem SGGZ wissen wir nun, dass die relative Häufigkeit der Gewinne nach $n$ Spielen für $n \rightarrow \infty$ gegen $p \approx 0{.}5177$ konvergiert (siehe Abbildung 8.1).

Abbildung 8.1: Relative Häufigkeit der Gewinne nach $n$ simulierten Runden des Würfelspiels aus Beispiel 8.2. Die rote Linie markiert die Gewinnwahrscheinlichkeit $p \approx 0{.}5177$.

In den vorangegangenen Kapitel haben wir die Verteilungsfunktion $F_X$ einer Zufallsvariable $X$ als wertvolle Charakteristik eingeführt. Außerdem haben wir zu Beginn dieses Kapitels die fast sichere Konvergenz als abgeschwächte Version der punktweisen Konvergenz von Funktionenfolgen kennengelernt. Somit stellt sich die Frage, ob wir die Konvergenz von Zufallsvariablen $X_n$ auch über die punktweise Konvergenz von Funktionenfolgen, bestehend aus den zugehörigen Verteilungsfunktionen $F_{X_n}$, beschreiben können. Tatsächlich ist dies möglich, führt aber (wiedermal) zu einem neuen Konvergenzbegriff.

Definition 8.2 (Konvergenz in Verteilung) Es seien $X$ und $X_n$, $n \in \mathbb{N}$ Zufallsvariablen mit zugehörigen Verteilungsfunktionen $F_{X_n}$ und $F_X$. Wir sagen, dass $X_n$ für $n \rightarrow \infty$ in Verteilung gegen $X$ konvergiert, falls \[\begin{align*} F_{X_n}(x) \rightarrow F_X(x) \text{ für alle Stetigkeitspunkte $x$ von $F_X$} \end{align*}\] für $n \rightarrow \infty$ und schreiben $X_n \stackrel{\text{d}}{\longrightarrow} X$.

Annahme 8.3

Streng genommen ist dies eine Konvergenz von Verteilungen $\mathbb{P}_X$ und keine Konvergenz von Zufallsvariablen. Allerdings nimmt man diese leichte Durchmischung von Begrifflichkeiten in Kauf, da Verteilungsfunktionen und Zufallsvariablen, wie wir wissen, sehr eng in Verbindung stehen.
Intuitiv lässt sich vermuten, dass, wenn Zufallsvariablen $X_n$ fast sicher oder in Wahrscheinlichkeit gegen $X$ konvergieren, auch die Verteilungsfunktionen der $X_n$ gegen die Verteilungsfunktion von $X$ konvergieren. Tatsächlich lässt sich dies auch beweisen. Die Umkehrung gilt allerdings nicht.
Insgesamt haben wir also \[\begin{align*} &\text{ Fast sichere Konvergenz} \\ \Rightarrow &\text{ Konvergenz in Wahrscheinlichkeit}\\ \Rightarrow &\text{ Konvergenz in Verteilung}. \end{align*}\]

Die Konvergenz in Verteilung lässt sich sehr gut visualisieren. Dies haben wir bereits in Beispiel 4.5 bzw. Abbildung 4.3 mithilfe von Histogrammen (als “grafische Approximation’’ einer Verteilung) demonstriert. In dieser Abbildung haben wir gesehen, wie die mit geeigneten Koeffizienten $a_n$ und $b_n$ zentrierte und normierte Summe von unabhängigen und identisch verteilten Zufallsvariablen $X_n$ gegen die Standardnormalverteilung konvergiert. In Zeichen haben wir gezeigt, dass \[\begin{align*} \frac{X_1 + \dots + X_n - a_n}{b_n} \stackrel{\text{d}}{\longrightarrow} Z, \end{align*}\] wobei $Z \sim \mathcal{N}(0, 1)$ eine standardnormalverteilte Zufallsvariable ist. Die konkrete Zentrierung $a_n$ und Normierung $b_n$ ist in Beispiel 4.5 mehr oder weniger vom Himmel gefallen. Nun haben wir sämtliches Handwerkszeug zur Verfügung, um die Koeffizienten beleuchten zu können. Diese ergeben sich aus einem der fundamentalsten Theoreme der Stochastik.

Theorem 8.3 (Zentraler Grenzwertsatz - ZGWS) Es seien $X_n$, $n \in \mathbb{N}$ unabhängige und identisch verteilte Zufallsvariablen mit $\mathbb{E}X_1 = \mu \in \mathbb{R}$ und $\text{Var}(X_1) = \sigma^2 \in (0, \infty)$. Dann gilt für alle $x \in \mathbb{R}$ \[\begin{align*} \mathbb{P}\bigg( \frac{X_1 + \dots + X_n - n\mu}{\sqrt{n \sigma^2}} \leq x \bigg) \rightarrow \Phi(x) \end{align*}\] für $n \rightarrow \infty$, wobei $\Phi$ die Verteilungsfunktion einer standardnormalverteilten Zufallsvariable ist.

Annahme 8.4

Die geeigneten Koeffizienten sind also gegeben durch $a_n = n\mathbb{E}X_1$ und $b_n = \sqrt{n\text{Var}(X_1)}$.
Betrachten wir unabhängige und identisch verteile Zufallsvariablen $X_n$, $n \in \mathbb{N}$, mit $\mathbb{E}X_1 = 0$ und $\text{Var}(X_1) = 1$, so besagt der ZGWS, dass mit $S_n = X_1 + \dots + X_n$ gilt \[\begin{align} \label{eq: KonvZGWS standardnormal} \frac{S_n}{\sqrt{n}} \stackrel{\text{d}}{\longrightarrow} Z \sim \mathcal{N}(0, 1). \tag{5} \end{align}\] Allerdings lässt sich zeigen, dass mit Wahrscheinlichkeit 1 \[\begin{align*} \limsup_{n \rightarrow \infty} \frac{S_n}{\sqrt{n}} = \infty \quad \text{ und } \liminf_{n \rightarrow \infty} \frac{S_n}{\sqrt{n}} = -\infty. \end{align*}\]

(Zur Erinnerung sei hierbei erwähnt, dass der Limes superior bzw. Limes inferior einer Folge von reellen Zahlen der größte bzw. kleinste Häufungspunkt ist. Im Falle von Funktionenfolgen ist dies punktweise zu verstehen.)

Somit kann man die Konvergenz $\eqref{eq: KonvZGWS standardnormal}$ nicht alternativ als fast sichere Konvergenz auffassen, da $\liminf \neq \limsup$. Allerdings wissen wir durch das SGGZ, dass \[\begin{align*} \frac{S_n}{n} \stackrel{\text{f.s.}}{\longrightarrow} \mathbb{E}X_1 = 0 \end{align*}\] für $n \rightarrow \infty$. Somit erkennt man, dass die Normierung einen entscheidenden Einfluss auf die Konvergenz(art) hat.

Dazu hat sich die Bezeichnung “Gesetze der großen Zahlen” für Grenzwertsätze mit Normierung $n^{-1}$ und “Zentrale Grenzwertsätze” für Grenzwertsätze mit Normierung $n^{-0{.}5}$ eingebürgert.

Eine Form, die zwischen diesen beiden Normierungen liegt, beschreiben die “Gesetze des iterierten Logarithmus’’. Diese nutzen eine Normierung der Form $\sqrt{2n\log\log n}$ und beschreiben das asymptotische Verhalten von $S_n$.